The Mass of the Photon
(1999)
Kristina Sviratcheva
Introduction
Particle or wave? The dual nature allows another description of the electromagnetic waves in terms of particles called photons. As a particle the photon can have a ³rest mass², it can carry energy and momentum. The photon mass is considered to be zero. This conception turns out to be very powerful in building the most significant theory in physics in the same way like so many laws are established on the foundation of a point charge or a point body. In reality we may ask if the mass of proton in rest is really zero, or at least zero within the uncertainties of a real experiment.
Recently, one of the most discussing problems concerns the question about the mass of neutrino. Although the interactions involved are different and therefore totally different experiments are performed, the approach to the answer is the same: looking for evidence that can occur in the case of non-zero mass. As far as the future physics can learn from its history it is important to see how the problem of the photon mass was approached.
Some experiments are made, which results are equivalent to the catching and weighing of a proton. None of them has proved the rest mass to be zero, and indeed such a proof may be impossible. An experiment that fails to find a photon mass does not prove the mass is zero; it merely shows that the mass is less than the limit of accuracy of the experiment. These limits have approached so close to zero, and the most recent values are exceedingly small. One can hope that the next experiments will reveal evidence of a definite, nonzero mass.
1.The Photon
A fundamental prediction of Maxwell¹s equations is that all electromagnetic waves travel in vacuum at a constant velocity c. The quantized electromagnetic field of frequency n is recognized as an assembly of photon particles with energy E=hn, where h is the quantum constant introduced by Max Planck. These light quanta travel with velocity c, and hence have zero mass. If the ³rest mass² were greater than zero, it would be possible to find a photon in rest and to measure its mass. To be consistent with the theory however the only restriction needed is that the mass is not large, so that we can be within the theory in the limit m®0. Perhaps it has a very small mass, much smaller than the electron, but still greater than zero. In that case the universe would differ only subtly from one containing massless photons, and only by detecting those subtle differences we can discover the photon rest mass.
The photon hypothesis is suggested in 1905 by Einstein in order to explain the photoelectric effect. The same year he published the special theory of relativity that is approached from the postulate, implied by the Maxwell¹s equations, that the light always travels with speed c, called velocity of light. He established a relation between the velocity v of a particle, its rest mass m and its energy E:
.
(1.1)
Therefore, for an object with a finite mass the velocity depends entirely on the energy, since all the other quantities are constant. Also, it gives the result that the velocity increases only by increasing the energy and for massive particles the velocity of light is unattainable. That is because if v=c then mc2/E has to be zero, which implies infinite energy.
For
a massless particle, however, mc2/E is always zero, regardless of the energy. Hence the particle always
travels with the speed c. It can
neither slow down nor speed up, no matter what is the energy. It however can
change its directions of motion.
Einstein assumed that photons are such particles but the theory of relativistic does not require that assumption. It is sufficient that c be related as a constant, the speed approached by any particle of finite mass as its energy increases without limit; c need not be the speed of light. If the photon has a mass then its velocity is dependent on its energy and
is always less than c. In a world with non-zero photon mass but zero neutrino mass the velocity of the neutrino would be c. It rules out the possibilities that strongly interacting particles could have one limiting velocity while electromagnetic interacting particles had another.
If the mass of the photon is not zero, another postulate can be adopted, which is equivalent to the Einstein assumption that there is a unique limiting velocity c for all phenomena. Given any two inertial frames, the first travelling at velocity v with respect to the second, there exists a frequency n0 depending on v and the desired accuracy e, such that any light wave of frequency greater than n0 in either frame will have a speed between c and c-e in both frames. The usual derivation of special relativity can now be applied using the Lorentz invariant limit ³n0 ®¥².
2. Maxwell Equations in the Massless Case
Maxwell¹s equations define the behavior of static electric and magnetic fields and predict the existence of electromagnetic waves. They are valid only if m=0.
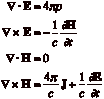(2.1)
The first equation (Fig.1), which embodies Coulomb¹s law, states that the number of the flux lines representing the electric field surrounding an isolated charged body is constant at all distances. As a result the number of lines per unit area, and hence the strength of the field, declines as the square of the distance. If the law is exact, the flux
Fig.2
Fig.1
lines continue indefinitely, that is, the number of lines remains constant at all distances from the charge (although the number of lines per unit area decreases as the square of the distance, giving the law for the electric force). Given a massless photon, the flux lines cannot stop until they meet another charge.
The second equation (Fig.2) states that the flux lines of a magnetic field always form a closed loop and therefore there are no isolated magnetic charges.
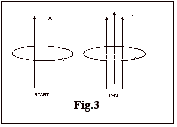The
third equation (Fig.3), which in-corporates the law of magnetic induction,
states that for any period of observation the average of electric field along a
closed curve is proportional to the increase in the magnetic flux passing
through the curve during that period.
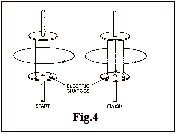The
fourth equation (Fig.4), which includes Ampere¹s law, states that the average
magnetic field in a closed curve is proportional to the sum of two terms: the
first term is determined by the total electric charge passing through the curve
and the second by the increase in the electric flux, again during the period of
observation. Here a voltage is applied to the plates of a capacitor; the
magnetic field can be considered to arise from either the current in the wire
(represented by the first term) or from the changing electric field (the second
term).
3. Non-zero Photon Mass
3.1 A World
with Massive Photons
If the photon is a massive particle there will be some direct consequences.
1) The first and most direct consequence of a finite photon mass is a frequency dispersion of the velocity of light. Even if the photon has a mass, electromagnetic waves consist of oscillating electric and magnetic fields. They are described by the third and the fourth Maxwell equations (2.1), which state that a moving magnetic field generates an electric field and vice versa. The assertion of a definite non-zero photon mass is equivalent to the specification of a free-electromagnetic wave by:
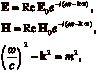(3.1)
where the last equation defines m in units of wavenumber, or inverse length. The group velocity then is:
.
(3.2)
Therefore, electromagnetic waves with different frequencies propagate with different speeds. High frequency electromagnetic waves move faster than low-frequency ones. As the frequency is reduced a limit is eventually reached for any given photon mass at which the velocity falls to zero. In other words, light stands still. This limit is attained when the wave has the frequency mc2/h. It is then no longer an oscillation in space but has the same amplitude everywhere. Its wavelength is infinite. With the present limits on the photon mass, however, that frequency is too low to be detected by known techniques.
2) The existence of longitudinal photon is the second consequence of nonzero m. Going to the Lorentz frame in which the photon is at rest, k=0, we see that there must be three independent polarization directions for a massive photon, since the plane transverse to k is undefined in this frame. The arguments fail for a massless photon since it can never have k=0. In the photon rest frame the electric field energy density E2 is proportional to photon intensity. However, the Lorentz transformations tell us that the field in a frame with photon frequency w will be very different for photon polarized ^ or || to k:
(3.3)
If m is much smaller than |k|, the field of a longitudinal (||) photon will be much smaller than that of a transverse photon by the factor of mc/w. Since power absorbed by electric charges is proportional to E2, we infer that scattering cross section of longitudinal photons will be suppressed compared to those of transverse photons by a factor (mc/w)2. This weak coupling explains how the longitudinal polarization, if it exists, could have escaped detection up to the present.
3) Another
consequence is the exponential decrease of static fields. For the limit of
static fields, we have 
, implying 
, hence, exponential decay of static fields with a range m-1. This behavior is familiar from
Yukawa¹s model for interaction of nucleons through pion exchange.
4) If the mass of the photon is not exactly zero then particles called magnetic monopoles do not exist. A monopole possesses a magnetic charge analogous to the electric one and its existence is by no means certain. Another argument is that quantum mechanics may not be valid over extremely long distances.
3.2 Postulates
Five postulates can be defined in the massive theory to count for the finite photon mass compared to the classical electrodynamics.
1) Assume that the electromagnetic field is defined through its action on a test charge q by the Lorentz force law:
.
(3.4)
This law determines the behavior of E and H under Lorentz transformations, that is they can be identified as independent components of the anti-symmetric four-tensor Fab by:
(3.5)
The force law in standard notation becomes:
,
(3.6)
where K is the Minkowski force in the four- dimensional space-time.
2) To assure invariance of the theory under the transformations of special relativity, it is required that the electromagnetic field at point x in space-time is linear in the charge and current densities, and the derivatives of these densities, all evaluated at earlier points x¢. This linear relation is Poincaré covariant (translation invariant and Lorentz covariant):
+terms with higher derivatives, (3.7)
which in the ³momentum space² has the form:
+terms with more factors of the 4-vector k . (3.8)
The quantity Dab/gd must be a Lorentz invariant tensor. And hence there are only two possibilities:
(3.9)
where eabgd is the completely anti-symmetric 4-tensor. Because of that D¢ produces a pseudo-vector E field, and a vector H field. Therefore the presence of D¢ implies parity violation or magnetic sources.
3) Assume that there is no magnetic sources or parity-violating term in the theory. Therefore, D¢ is zero.
4) Assume that the dependence of the theory on a small photon mass be such that as m®0.
5) Assume that there exists a locally conserved energy-momentum density, such that energy and momentum of a system of charges and fields is conserved.
The requirements of Poincaré invariance (including parity) are sufficient to deduce the homogeneous Maxwell equations, which may be written:
.
(3.10)
This means that the fields may be
derived from 4-vector potential 
:
.
The properties of the Lorentz invariant tensor D, determined by the postulates, yield the ordinary inhomogeneous Maxwell equation, modified by the addition of m2:
.
(3.11)
In four-dimensional Minkowski space the modified Maxwell equations can be written as:
( 
.
(3.12)
The free solution (J=0)
of the last equation obeys the relation 
.
Introducing the vector potential Aa , Maxwell-Lorentz equations follow:
( 
,
(3.13)
where the last equation gives the Lorentz gauge.
Finally the Proca equation for a massive vector field coupled to a conserved current can be written in the form:
(3.14)
The whole effect of introducing a finite photon mass is to introduce at each point x a spurious current proportional to the vector potential and thus a function of the true current at many earlier points x¢. In three-dimensional notation the massive Maxwell equations become:
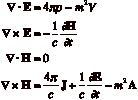(3.15)
with A and V the space and time components of the 4-vector potential Am. Proca¹s equations predict modified fields. The electric field no longer diminishes as the square of the distance but falls off exponentially. Flux lines can now fade away even in empty space, and at great distances the field effectively vanishes.
The
magnetic field declines exponen-tially with the distance and also changes
shape, being compressed at the magnetic equator. These modifications imply a
characteristic length scale for electro-magnetism determined by the photon
mass.
The
freedom of gauge invariance found in conventional electrodynamics is completely
lost here. The Lorentz gauge,
, implies freedom in choosing Aa
with an additional term
, where l is a scalar function. This does not change Fab
but the Lorentz gauge condition implies l=0. At the same time, if A is
already a solution of the
Proca equation we have the contradictory requirement ( +
0 , satisfied
only if l
is a constant. Hence, all freedom of gauge change is lost. It can be seen by
the fact that in the Maxwell-Proca equations the potentials themselves have
physical significance, not just through their derivatives.
The fifth postulate implies energy-momentum density conservation law:
,
(3.16)
where T is the energy-momentum density tensor for massive electro-magnetic field and matter.
The basic symmetry principles of special relativity, the assumption that fields are linear functions of currents, and the postulate of energy conservation imply that the classical electrodynamic theory can be modified in only one way - replacing the Maxwell equation by the Proca equation to account for possible small photon mass.
In
fact, the most common technique for deriving massive electrodynamics is the use
of a Lagrangian density by simply adding to the m=0 Lagrangian a ³photon mass term² proportional to
. This is the most general modification, which vanishes as m®0 and involves only local coupling (all fields evaluated
at the same point in space-time). The Lagrangian approach embodies all of our
postulates (1-5).
4. Terrestrial Limits
4.1. Measurements of c
The most straightforward way to obtain a limit on the photon mass is to look for a variation in c over the spectrum.
The possibility of observing the light at a standstill would seem to offer an obvious and dramatic method of measuring the photon mass. In order to verify that the wave is stationary we must observe it in a region whose dimensions are large compared with the wave length the radiation would have if it moved with the speed c. That wavelength is equal to c/n, or h/mc (nmin=mc2/h). Present experimental limits on the photon mass give a ³rest frequency² of less than about one oscillation every 10 seconds. A numerical calculation shows that the corresponding wavelength is more than 400 times the radius of the Earth. Unfortunately it would be difficult to search for such slow oscillation over such large distances.
The difference between the long-wavelength light velocity and the short-wavelength limit (|v |=c) is:
(4.1)
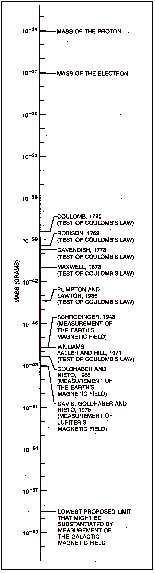
The velocity is measured to an accuracy of one to ten parts in 106 over much of the electromagnetic spectrum. The lowest frequency measurement with such precision is that at n=173MHz (l=1.73m). The one in 105 accuracy of this measurement implies m£6´10-42g. Because the effect is quadratic in wavelength one can improve considerably on this number by going to lower frequency, even if the measurement is less accurate.
In the 1930¹s, Mandel¹shtam, Papalexi and their collaborators developed a tech-nique for measuring the velocity of long radio waves. A radio wave of a frequency n is sent from a transmitter to a receiving station far away. At the receiver, a wave of frequency (3/2)n, for example, is synchronized with a transmitter to a received wave transmitted back to the original station. The phase lag of the return wave with respect to the original signal has calculable contributions, including effects of the apparatus at both ends, plus a term proportional to the time of travel.
Al¹pert, Migulin and Ryazin (1941) used this technique to measure the dispersion of long (³100m) waves travelling over a land and a sea. Over land the dispersion was quite large (»1%), but over sea they measured a velocity shift of 7´10-4 between 300-450m. If this is interpreted as a photon mass effect, it corresponds to mass limit m£7´10-6cm-1=2´10-43g. It is possible that the result of Al¹pert was due to instrumental error. It would be difficult to improve enormously on their work because of irregularities in the medium through which the wave propagates (the Earth or its atmosphere).
Comparison of the results here with those of other methods is not encouraging.
4.2
Deviation from Coulomb¹s Law
In 1788 Coulomb published his experimental results having measured both attractive and repulsive electric forces that have the mathematically expression by the equation:
,
(4.2)
where F is the force between the charges, e1 and e2, and r is the distance between them.
In 1755 Benjamin Franklin observed that a
cork ball placed inside an electrically charged metal cup is not attracted to
the inside surface of the cup. In order to explain the phenomenon Prestley
recalled Newton¹s reasoning in deriving the inverse square law of gravitation.
Newton had shown that a uniform spherical shell of matter would exert no
gravitational forces on objects inside it, provided that the gravitational
force declines as the square of the distance. Pristley made the inference that
the phenomenon he had observed is in some way similar and thus the electric
force too should obey an inverse square law.
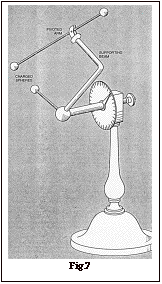
The first quantitative test of Coulomb¹s law is made in 1769 by John Robison (Fig.7). His apparatus balances the repulsive electric force between two charged spheres against the gravitational torque on a pivoted rod. By adjusting the angle of the supporting beam the force can be measured at several distances. It can be calculated,
knowing the weight of the rod and thus the agreement of the results with the inverse square law can be tested. Robison expressed the results in terms of a possible deviation from Coulomb¹s law in the form of a modified equation:
.
(4.3)
If q is found to be zero, the inverse square law will be exact. He obtained a value for q of 0.06. It implies a limit on the photon mass of m»4´10-40 g.
In 1773 Cavendish conducted an experiment (Fig.8), also suggesting the influence of Newton¹s ideas about gravitation, with two concentric metal spheres connected by a conducting wire. The outer sphere is given an electric charge, then the connection between the spheres is broken and the inner sphere is tested for charge. If the inverse square law is exact there should be no charge in the interior of the larger charged sphere. If the law is not exact some charge can be expected to migrate through the wire to the smaller inner sphere. Cavendish placed a limit on the magnitude of q equal to 0.02. Later interpretations of Cavendish¹s results give a limit on the mass of the photon that is a little
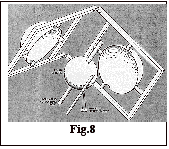greater than 1´10-40 g. All
subsequent improve-ments in the testing of the inverse square law are made
through variations of Cavendish¹s method. Cavendish
technique is a powerful one because it is a Œnull experiment¹. A small
deviation from the inverse square law will lead to small fractional changes in
the observations of Robison and Coulomb, but Cavendish needs only to find out
whether a charge is present or absent. It
is much easier to make a yes-or-no
determination than it is to achieve high accuracy in each of the series of measurements of some nonzero
quantity such as the electric field at various distances from a charged body.
Cavendish¹s value for q is improved in 1873 by Maxwell, who showed that q is no greater than 1/21 600. The only modification is that the outer sphere is grounded instead of removed, and the inner globe is tested for charge through a small hole.
Coulomb¹s law can be interpreted geometrically by imagining an electric charge isolated in empty space, radiating lines of flux in all directions. Given a massless photon, the flux lines cannot stop until they meet another charge. If the photon has a mass, on the other hand, the lines of flux fade away in empty space. At a large distance the electric field is effectively extinguished.
The rate at which the field decays is determined by the characteristic scale of length associated with the mass of the photon. This length can be derived from the equations relating energy, frequency and velocity in quantum mechanics, and it is found to be equal to h/mc; since h and c are constants, the scale is defined entirely by the mass. For an isolated electric charge the flux reduces about 600-fold each time the distance from the charge is increased by an amount h/mc. The relation of field intensity to distance is thus an exponential one. This result is familiar in the wider context of particle physics, where a more general rule states that the range of a force is inversely proportional to the mass of the particle that transmits it. The strong or nuclear force that acts between protons and neutrons has a quite short range: about 10-13 cm. From that fact Yukawa predicted in the 1930¹s that the quantum of the strong force will have a mass roughly a tenth that of the proton; one such particle, the pion, is discovered in the following decade, and its mass is near the predicted value. The experiments prove the same for the particles that transmit the weak force (W±, Z0), that is responsible for certain radioactive decays with an even shorter rage (10-16 cm). This law of proportionality predicts that if the photon is massless, the range of the electromagnetic force must be infinite. If it should be found to have mass, however, the influence of a stationary charge or of a steady current would be effectively confined to a sphere of a finite radius. These conclusions do not apply to the propagation of free electromagnetic waves.
The Cavendish experiment is entirely capable of detecting the exponentially decreasing field that will be associated with a massive photon. The experiment is based on the notion that the interior of an electrically charged conducting sphere will be free of charge only if the electromagnetic force obeys an exact inverse square law. A law of exponential decrease obviously departs from the inverse square law, so that the experiment should be a sensitive indicator of photon mass.
The
Plimpton-Lawton experiment of 1936, reinterpreted according to these
principles, yields a limit on the photon rest mass of 10-44 g. They
performed an improved version of the Cavendish-Maxwell experiment. Two concentric
spheres of radii a=2.5ft, and b=2.0ft are grounded, and then the outer sphere
is charged to V=3000V. Actually, for technical reasons, the voltage is
quasistatic, having a frequency of 130 cycles/min. A galvanometer which
connects the two spheres and which can be observed through a conducting window
indicates DV=F(a)-F(b)<10-6
V. Using the Maxwell theory (1873) and the equation 
in the static
limit, giving the solution for the massive scalar potential between the two
spheres 
, Plimpton and Lawton¹s experimental result sets the limit
.
The measurements have been repeated several times by various groups of investigators, with ever increasing precision. Better limit obtained by the Cavendish
method is reported in 1971 by E.R. Williams, J.E.Faller and H.A.Hill, who employed five electric shells instead of two in order to improve the sensitivity and to help eliminate errors introduced by stray charges (Fig.9).
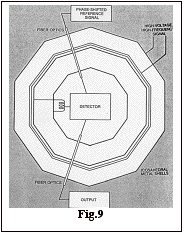The
shells are icosahedrons (icosahedral). A high voltage, high frequency signal is
applied across the outer two shells, and a sensitive detector is employed to
search for any trace of this signal appearing across the inner two shells. The
detector operates by amplifying the signal from the inner shells and comparing
it with a reference signal that is identical with one applied to the outer
shells but that is shifted in phase at a rate of 360 degrees per half-hour. Any
signal in the output of the detector that has a period of a half-hour is then
evidence for a violation of
Coulomb¹s law. To avoid introducing extraneous fields the reference signal and the output of the detector are transmitted through fiber optics.
Aside from advances in quality of available equipment, the first essential improvement is the use of a ³lock-in² detector to observe oscillations in the DV in synchronism with oscillations in the applied potential V. The second improvement is to increase the oscillation frequency, reducing thermal, or Johnson, noise in the relevant frequency band: the Johnson noise in the input to the amplifier is proportional to the temperature, the frequency bandwidth (or reciprocal of the observation time), and the real part of the impedance:
.
Here R is the input resistance, C is the parallel capacitance, and w/2p is the frequency. The limit is for large w. Thus the root mean square noise voltage is inversely proportional to the frequency.
The values of Williams, m£6´10-10cm-1=1.7´10-47g, may still improve. It represents one of the best laboratory limits.
To estimate the ultimate limits on the Cavendish method, let us consider possible improvements on the experiment of Williams. First, one can reduce the Johnson noise voltage by increasing the time of observation (or using a low temperature, but cooling such a large apparatus to liquid helium temperature is a formidable task). Thus, by running the experiment for a year, the mass limit will be comparable to the geomagnetic value (and 5 times better than the present result). Secondly, one can increase the frequency, reducing Johnson voltage in proportion. One can imagine other improvements: increasing the applied voltage, increasing the input resistance (this reduces Johnson voltage), and increasing the dimension of the apparatus. The first and second of these cause large increase in power requirements. The third appears most promising because the limit on m goes inversely as the diameter of the spheres. An optimistic guess leads a final limit 40 times smaller than the present geomagnetic value.
5. Extraterrestrial Limits
5.1.
Dispersion in the Speed of Starlight
A limit on the photon mass can be obtained by measuring the difference in time of arrival of radiation of different frequencies with the same origin. For example, if blue and red light rays come from the same event, the difference in time of arrival is:
.
(5.1)
De
Broglie in 1940 suggested that this method could yield a mass limit by using
light from a star emerging from behind its dark binary companion. DeBroglie
considered the case
, L=103
light years, and
. Then the limit is estimated to be: 
However, even if one takes advantage of the wider spectrum observations and faster electronics now available, this method is intrinsically limited. In 1963 Gintsburg gave a number of reasons, but the crucial one is the natural dispersion of light traveling through the interstellar plasma in a magnetic field.
Despite this limitation, as Feinberg (1969) has pointed out, the observed dispersion in arrival time of radio signals from pulsar provides the best ³dynamic² test of the photon mass (velocity-dispersion limit) up to then. If the dispersion is partly a photon mass effect, for radiation from the Crab pulsar NP0532 we have m£3´10-7cm-1=10-44 g.
Feinberg also has made the interesting point that the pulse arrival times show no sign of any dispersion, except that implied by the photon mass effect over the whole range of frequency from radio to optical.
Feinberg has mentioned the possibility of observing pulsar signals from another galaxy. This is not very promising. The first is because the distance to the nearest galaxies is of the order of 50x103kpc (about 5 times the distance to the Crab nebula pulsar). This means that the signals will be down by the factor of 2500. Thus, a successful pulsar search will probably have to depend on a statistical analysis of radio signals rather than on the direct observations that are needed for a massive limit. Further, even if a pulsar could be observed directly, on the average the signals would have to travel through about 1 000 kpc in each galaxy. Thus, even if intergalactic space were empty of plasma, the plasma dispersion in the galaxy would limit the improvement in the mass limit from pulsars to a factor of only 5, so that the ultimate mass limit from pulsars is about 500 times worse than the present geomagnetic value.
It would be interesting to see if the low frequency pulse broadening and/or intensity oscillations with w became more noticeable for such a distant pulsar.
5.2. Magnetostatic Effects
Magnetic fields are superior indicators of the photon mass because they extend over large distances. They can be studied over vast distances and examined for alteration of form that could be attributed to a nonzero photon mass.
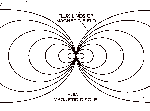
Schrödinger (1943), following an observation of McConnell, proposed a method using the Earth¹s static magnet field that has yielded one of the best photon mass limits. The quantitative effect of a photon mass m on static fields is to cause an extra ³Yukawa² decrease in field strength as e -mr, where r is the distance from the source. However, in the massive electrodynamics, Ñ· H=0 . This is simply a consequence of reflection symmetry in electrodynamics and the absence of magnetic sources. The magnetic dipole field of the Earth H has vanishing divergence, which means that the flux in each field line is conserved. Now a field line is farther out at the magnetic equator than it is near the pole. Hence, the Yukawa exponential decrease affects the field line most at the equator. To keep constant flux, the field pattern must change shape, allowing flux lines to move in somewhat at the equator. This compression of the equatorial field lines has the effect, on a sphere of fixed radius, of increasing the field at the equator relative to the field at the pole. The effect is the same as that of a constant external field parallel to Hequatorial. In fact, the field of the Earth is not pure magnetic dipole. In the absence of true external currents, that can produce a uniform field over the surface of a sphere, the average of any component of H over this sphere must vanish. Therefore, if such currents were estimated, detection of anomalous uniform ³external² field on the surface of the Earth would demonstrate a violation of Maxwell¹s theory of just the form produced by a finite photon mass.
The quantitative derivation of the external field effect is based on the static Proca equation for the vector potential:
,
(5.2)
which gives the solution:
,
(5.3)
where:
(5.4)
is a magnetic dipole moment. Since H is Ñ´A, the dipole contribution to the Earth¹s field, measured from coordinates centered at the dipole (in the usual physics convention, this dipole points to the Southern Hemisphere), is:
, (5.5)
where HD is the ordinary non-massive dipole field.
If observations are made near the surface of a sphere centered at the dipole (here it will be the surface of the earth r»R= constant), the factors in the first term of H will make D appear to have a slightly different value when compared to HD. However, the last term is new. It will be observed as an apparent external magnetic field anti-parallel to the direction of the dipole. The ratio of the ³external² field ( Hext ) to the dipole field at the equator (HDE ) is :
.
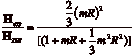(5.6)
Using the 1922 magnetic surveys discussed by Schmidt (1924), Schrödinger obtained a ratio of Hext /HDE =539g/31089g, where g=10-5 G and putting this in (5.6) yields m£5.5´10-10cm-1=1.9x10-47 g.
In fact the ingenuity of the external field method is precisely that it requires only ground observations. However, the more recent work on the geomagnetic limit on m does exploit satellite data as well as earth-based measurements. Furthermore, Schrödinger method might be applied to other planets.
In 1968 Goldhaber and Nieto improved on this results by using Cain¹s fit to geomagnetic data from earthbound and satellite measurements. They gave an upper limit on the anti-parallel external field, which can be due to a finite photon mass, Hext£20g.
The
significance of this limit depends crucially on the reliability of the fit of
Cain to the geomagnetic field. For these reasons, the possibility of systematic
errors in the fits to a particular spherical-harmonic coefficient of many tens
of g
cannot be excluded. Taking account of this, the mass limit is evaluated to be: 
This is five
times better than the number that Schrödinger suggested on the basis of much
less precise and very much less reliable data. Also, this is the best limit for
this method.
From the discussion of the Schrödinger method applied to the Earth¹s magnetic field, it seems more unlikely that an improvement of more than a factor of 2 in the limit on m could be achieved. Other two alternative objects for magnetic measurement are the dipole fields of the Sun and of Jupiter. The Sun has the advantage of large size, but the disadvantage of enormous and rapidly varying plasma currents, which make accurate magnetic surveys quite difficult. Also, the relevant region is very hot.
Jupiter is about 11 times larger in radius than the Earth, and has a magnetic field ten to 1 000 times as strong at the planetary surface. The Jovian magnetosphere appears to be 40-50 Jovian radii from the planet, while the Earth¹s magnetosphere is at 8-10 radii. As a consequence, one may expect a low charge and current density out to a much larger distance, in Jovian radii, than holds for the Earth, measuring in Earth radii. The higher field, the larger radius, and the enormous magnetosphere should make an improvement of a factor ten on the geomagnetic limit quite easy with orbiting satellite magnetometer data. The main potential difficulty would be rapid fluctuations in field during satellite orbits. The large magnetosphere would make the altitude-dependent method more useful than it is for the geomagnetic limits.
The
upper bound on the photon mass m£8´10-49g
derived from the measurements of Jupiter¹s magnetic field is by no means the
smallest that can be achieved. One possibility of improving on it is through
observations of even larger magnetic fields, such as the field of the galaxy.
Yamaguchi proposed that a photon mass limit could be obtained from magnetic fields detected in astronomical observations. His idea was that if fields extend over a distance D then the photon mass must be m<1/D. Using the dimension of the Crab nebula, he deduced m<10-17 cm-1. The same technique, applied to the field in one of the spiral arms of our galaxy, could yield a limit m<10-21 cm-1.
In
any cases, future ³experiments² in Galactic magneto-hydrodynamics will improve
mass limit, depending on the detailed character of the results, ranging from 10-14
cm-1 to the Yamaguchi limit 10-21 cm-1. The last number represents the ultimate possibility for an
improvement limit among suggestions we have seen.
5.3 Altitude-Dependent Method
One
might hope to use satellite measurements at varying altitudes to detect the
exponential decay of H. From (5.6) the
magnitude of the dipole field for m ¹0
is: 
, where 
.
Gintsburg first applied the altitude-dependent method, and he used the assumption F=1-(mr)2 to obtain a mass limit from magnetic measurements at varying altitudes by Vanguard, Explorer, and Pioneer satellites. He gave a limit m<(8-10)´10-48 g. Thus, it is nearly a geometric mean between the old and the new results of the Schrödinger method. The main limitation on the altitudedependent method is that external perturbations become quite significant beyond ~3R.
5.4 Eccentric Dipole or ³Vertical Current² Effect
In his early paper, Schrödinger (1943) has pointed out an effect due to the displacement b of the magnetic dipole origin from the geocenter. From (5.3), the lines of vector potential are circles around the magnetic dipole axis, and hence would intersect the surface of the Earth at a small angle of order |b|/R~1/19. From (3.15) follows that there is a ³feigned² vertical current from the component of A perpendicular to the Earth¹s surface. That is, the integral of H along a closed path on the surface would fail to vanish H could not be written as the gradient of a scalar potential. To look for this effect, Schrödinger consulted Schmidt¹s (1942) vertical current measurements for the independent surveys of 1885 and 1922. Schmidt had generally found ascending currents in the Eurasian-African hemisphere, and descending currents in the American-Pacific one in 1885. These signs are in agreement with the effect of a finite m. However, the later survey indicates that the currents were smaller and fluctuated in sigh from point to point within the same hemisphere. This eventually caused Schmidt to doubt his earlier ³hemisphere current effect².
However, there is a more elementary reason for giving up this approach. The effect produced by a massive photon via its ³eccentric dipole² compared to that produced via its ³external field² is intrinsically smaller by a number of order (|b|/R), which for the Earth is ~1/19. Thus, the ³eccentric dipole effect² will not yield as good a mass limit as that which could be obtained by a similar experimental effort using the ³external field effect², even if the real currents could be separated out.
5.5. Long-Period Magnetic Waves
Another approach is through observing of magnetic waves in a highly conductive medium, such as an ionized gas, or plasma. The velocity of such waves is determined by the properties of the plasma, and if the photon is massless, the velocity is independent of frequency. If the proton is massive, low-frequency waves are retarded, and there is a limiting frequency below which the waves cannot propagate at all. The existence of low-frequency magnetic waves implies an upper limit on the photon mass.
Gintsburg (1963) proposed a method to limit the photon mass that deals with the propagation of long period magnetic waves. The idea focuses on the form of the index of refraction (n=|k|c/w) of electromagnetic radiation in a cold, non-dissipative, magnetized plasma. There are two types of magnetic waves in such plasma. In the first, or acoustic type, the wave propagates perpendicular to the direction of the static magnetic field H0, and the oscillating field points in the same direction as H0. The second, and purely magnetic, wave is the Alfvén wave, in which the magnetic field oscillates perpendicular to H0 and the wave travels in the plane perpendicular to the oscillating field, at an angle q to H0 . To introduce finite photon mass, m2 is subtracted from the right-hand side of the dispersion equations for both cases. In fact this procedure can be justified by introducing the Proca equations (3.15) in place of Maxwell¹s, and following the modifications in the standard derivations of the dispersion equations .We have:
(magnetosonic),
(Alfvén), (5.7)
where VA is the Alfvén velocity
, and r is the mass density. For m¹0, k2 becomes negative for low enough w, so that the waves will be damped. In
principle, if the critical frequency at which the waves do not propagate can be
found, the photon mass can be measured directly. The lowest mass that can be
measured for any given frequency or period T will be
,
(5.8)
no matter what the plasma density or field strength.
Patel
in 1965 proposed a mass limit from this idea. He combined ground magnetometer
and Explorer XII results to obtained the mass value 
, which he took as the upper limit to the photon mass.
There are numerous reasons for questioning this value: uncertainties in the values assumed for the plasma density and the magnetic field strength. Yet there obviously is huge uncertainty in the assumption that the damping came from a massive photon, and not from other dissipative mechanisms.
To sum up, although this idea is very interesting, a convincing mass limit would require the solution of many difficulties.
6. Longitudinal Photons
Non-zero photon mass implies the existence of a third degree of freedom for the proton: longitudinal polarization. This immediately suggests potentially significant effects, of which the most dramatic is a fifty per cent increase in thermodynamic equilibrium with a reservoir at temperature T. Since Plank¹s radiation law is known to be precise, this effect is not present. The answer to this was given by Bass and Schrödinger in 1955 who had pointed out that the approach to equilibrium of longitudinal photons in a cavity is very slow, having a time scale comparable with the age of the Universe. Even with the highest densities and longest time scales known, longitudinal photons would have negligible effect on thermodynamic system.
The possibility of detecting longitudinal photons is an intriguing one. For example, if a capacitor is placed inside a conducting sphere, any incident longitudinal waves will pass through the sphere and deposit a small fraction of its energy in the capacitor. Capacitors outside the sphere would receive comparable energy, but for transverse waves they will receive much more than the shielded capacitor. The difficulty with this suggestion lies in conceiving of a sufficiently powerful source for L -waves. The Sun is the most obvious candidate. A rough estimate indicates that the L-wave radiation arriving at the Earth will produce a root mean square voltage across a capacitor with 1m2 area about 105 times smaller than the Johnson noise across the capacitor. Thus the chances of observing thermal longitudinal photons are indeed remote.
The reaction or emission rates for longitudinal photons are suppressed by a factor (mc/w)2 compared to those for transverse photons (3.3) remains true for almost all quantum transitions in atomic or smaller systems. In fact, a transition between two states, each with angular momentum zero, cannot proceed by emission of a single photon. It can go by L-wave mission that is so slowly that double-photon emission is much more likely. In this case the rate of such transition is suppressed by a factor of (ma)2 compared with an allowed electric dipole transition of the same frequency. Here a is a characteristic (length) dimension of the quantum system in question.
If
transverse and longitudinal transition matrix elements are comparable, then
amplitudes for absorbing or emitting longitudinal photons are suppressed by (mc/w),
and rates or cross sections are suppressed by the square of this factor. In the
classical (Thompson) limit, transition matrix elements are independent of
direction, and suppression factor is exactly (mc/w)2.
The only way to get large longitudinal cross section is to have much bigger
matrix elements for longitudinal currents, that is more longitudinal- than
transverse-photon induced transitions.
In fact, if longitudinal photons exist, their observation will be difficult if not impossible, and their effects are negligible, even on an astronomical scale.
7. Present and Future Experiments
Boulware and Deser in 1989 used the Aharonov-Bohm effect to investigate the photon mass. The experiment probes the deviation of the magnetic field from its classical value at short distance. The precision is obtained only because it is a null experiment for m=0, combined with the use of large magnetic fields and the sensitivity obtainable by detecting phase shift. Photon mass limit is estimated as m£10-7cm-1.
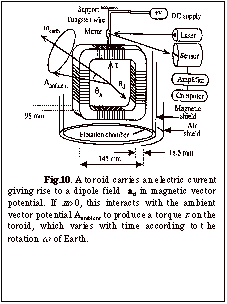
In 1997 Lakes performed a novel experiment, based on a toroid Cavendish balance and estimates the product of photon mass squared and the surrounding cosmic magnetic vector potential A, rather than m itself, because values of A inferred from astrophysical fields are uncertain. The method is based on the energy density of the vector potential in the presence of photon mass, not on measurement of the magnetic field. This approach gives (Am2)<2´10-9Tm/m2 and sets photon mass limit m£0.5´10-12cm-1. The present simple apparatus is more sensitive than prior experiments because it makes use of estimates of large-scale cosmic magnetic fields, which are associated with very large vector potentials.
Among the possibilities for other observable effects are: detection of longitudinal waves from coherent astronomical source, production and scattering of very high energy longitudinal photons through unexpectedly enormous longitudinal current matrix elements, measurements of velocity dispersion for low frequency radiation in intergalactic space.
Conclusions
In
the ancient Greek philosophers asked the question about the matter that builds
our world. They first came with the idea that all the nature is consistent of
discrete units. They called them atoms because the wise men considered them the
smallest inseparable particles. They began to describe the atoms by such
characteristics as mass and dimension. But it turns out that the atoms have
structure and there exist even smaller particles, like electron, proton, neutron.
The first experiments that measured their masses were performed. Later on it
appears that we can ³observe² even smaller particles, going in the depth of the
mysteries of physics. Now it is a proven fact that even such particles as
nucleons are not elementary: they consist of quanta called quarks. In fact,
nobody knows whether we shall be able to ³observe² any real elementary
(structureless) par-ticles. Maybe the famous Zannon¹s arrow paradox becomes
reality when the physical experiments begin to deal with smaller and smaller
objects in the same way as the arrow always travels just the first half of the
distance never reaching the aiming point.