Computer-Generated Holography (CGH)
PHYS4412 (Computational Science II)
Department of Physics & Astronomy
Louisiana State University
PHYS4412 (Computational Science II)
Department of Physics & Astronomy
Louisiana State University
| III.C | Triangular Aperture |
|---|
Setup
Consider any three points in space -- P0, P1, and P2 -- that do not lie on a straight line. From elementary Euclidian geometry we know that these three points define a plane. They also can be used to specify the vertices of a flat triangular aperture that lies in this plane.
| Figure III.1 |
|---|
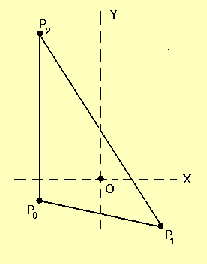 |
| P0 | = | ( 0, 0, 0 ) , |
| P1 | = | ( X1, Y1, 0 ) , |
| P2 | = | ( 0, Y2, 0 ) . |
(Note that, defined in this way, X1 and Y2 are necessarily positive numbers, but Y1 may be either positive or negative.) Finally, shift the Cartesian coordinate system sideways in the X-Y plane so that P0 is no longer at the origin but is, instead, at the position,
| P0 | = | [ - ( X1 / 2 ) , - ( Y1 / 2 + Y2 / 4 ) , 0 ] , |
as illustrated in Fig. III.3. (The rationale for shifting the origin of the coordinate system to this position will be given below.) As a result, the other two points will be located at positions,
| P1 | = | [ ( X1 / 2 ) , ( Y1 / 2 - Y2 / 4 ), 0 ] , |
| P2 | = | [ - ( X1 / 2 ) , ( 3 Y2 / 4 - Y1 / 2 ), 0 ] . |
We will henceforth refer to the Cartesian coordinate system defined in this way as the aperture coordinate system. In the aperture coordinate system, the equation for the line that connects vertices P2 and P1, and thereby forms the "upper" edge of the triangular aperture is,
| Y = [ ( Y1 - Y2 ) / X1 ] X + Y2 / 4 , |
and the equation for the line that connects vertices P0 and P1, and thereby forms the "lower" edge of the triangular aperture is,
| Y = [ Y1 / X1 ] X - Y2 / 4 . |
Analytical Result
By analogy with earlier chapters, if the triangular aperture is assumed to be uniformly bright (i.e., aj,k = a0 dX dY, and a0 is the brightness per unit area), and the phase f = 0 at all locations on the aperture, then at any position in space (Xa,Ya,Za) as measure in the aperture coordinate system from the aperture origin (as illustrated above in Fig. III.3),
| A (Xa,Ya,Za) | » | A0 a0 | ò | exp{ - i [2p XaX / (lL)]} dX | ò | exp{ - i [2p YaY / (lL)]} dY , |
| L | º | [ Xa2 + Ya2 + Za2 ]1/2 . |
Both of these integrals can be completed in the same fashion as described in earlier chapters for the 1D slit or for the 2D rectangular aperture, but now some care must be taken in establishing the limits of integration because along two of the edges of the triangular aperture, the limiting values of "Y" are now a function of the X-coordinate. However, these functions are readily specified for the "upper" and "lower" edges of the triangle by equations (4) and (5), respectively. Hence, the integral over Y must be performed between the limits Ylower and Yupper, where,
| Ylower | º | Y1 ( X / X1 ) - ( Y2 / 4 ) , |
| Yupper | º | ( Y1 - Y2 ) ( X / X1 ) + ( Y2 / 4 ) , |
and the integral over X must be performed between the limits Xlower and Xupper, where,
| Xlower | º | - X1 / 2 , |
| Xupper | º | + X1 / 2 . |
Completing the integrals with these limits gives,
| A (Xa,Ya,Za) | » | i [ A0 a0 ( X2 Y3 / 2 ) ] { | [ exp( - i b ) / ( 2 b ) ] sinc aupper |
| - | [ exp( + i b ) / ( 2 b ) ] sinc alower } , | ||
where,
| aupper | º | p Xa ( l L )-1 [ X1 + ( Y1 - Y2 ) ( Ya / Xa ) ] , |
| alower | º | p Xa ( l L )-1 [ X1 + Y1 ( Ya / Xa ) ] , |
| b | º | p Ya ( l L )-1 [ Y2 / 2 ] . |
Discussion
Now, when comparing equation (10) to equation (I.B-7) -- which is the result for a rectangular aperture -- we see two key differences. First, because aupper is not equal to alower, we are unable to combine the terms containing b into a sinc function. (See, however, what happens when Ya = 0, as discussed below.) Second, equation (10) does not contain a phase offset factor in either the X or Y coordinate directions analogous to the terms that contain Q1 and J1 in (I.B-7). Terms of this nature do not appear here precisely because of our strategic positioning of the origin of the aperture coordinate system as illustrated in Figure III.1 and defined by equation (2).
The analytical expression (10) formally poses problems when either Xa = 0 or Ya = 0 ( b = 0 ) because of division by zero. However, equation (10) still provides the correct result if we realize that, when Xa = 0,
| aupper | —> | p Ya ( l L )-1 [ Y1 - Y2 ] , |
| alower | —> | p Ya ( l L )-1 [ Y1 ] . |
When Ya = 0, one can show that equation (10) reduces to the simpler expression,
| A (Xa,0,Za) | » | A0 a0 ( X1 Y2 / 2 ) | sinc [ p Xa X1 ( l L )-1 ] . |
Finally we note that, via the general coordinate transformations derived in § II.C, we can now use equation (10), above, to specify the complex amplitude of light at any coordinate location on a holographic screen. When employing these coordinate transformations, care must be taken to define the offset coordinates (XO,YO,ZO) shown in Figure II.3 in terms of the separation between the origin (usually the center) of the hologram and the particular origin of the aperture coordinate system, as specified above. Then, for example, if XO = YO = 0, equation (II.C-4) provides the functions Xa(xh,yh), Ya(xh,yh), and Za(xh,yh), that are required to express the distance L and the angles aupper, alower, and b entirely in terms of coordinate positions across the hologram.