Computer-Generated Holography (CGH)
PHYS4412 (Computational Science II)
Department of Physics & Astronomy
Louisiana State University
PHYS4412 (Computational Science II)
Department of Physics & Astronomy
Louisiana State University
| I.A | One-Dimensional Aperture Oriented Parallel to the Image Screen |
|---|
General Concept
Consider the amplitude (and phase) of light that is incident at a location y1 on an image screen that is located a distance Z from a slit of width w. First, as illustrated in Figure I.1, consider the contribution due only to two rays of light: one coming from location Y1 at the top edge of the slit ( a distance D1 from point y1 on the screen) and another coming from location Y2 at the bottom edge of the slit (a distance D2 from the same point on the screen).
| Figure I.1 |
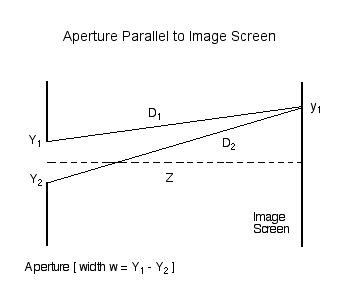
|
The complex number A representing the light amplitude and phase at y1will be,
| A (y1) | = | a( Y1 )exp[i(2p D1/ l + f1 ) ] + a( Y2 )exp[i(2p D2/ l + f2 ) ], |
where l is the wavelength of the light, a( Yj ) is the brightness of the light at point Yj on the aperture, and fj is the phase of the light as it leaves point Yj.
Now, if we consider for the moment that at all locations on the aperture Yj , the light has a brightness a( Yj ) = 1.0 and a phase fj = 0.0, then,
| A (y1) | = | A0 { 1.0 + exp[i(2p / l ) ( D2 - D1 ) ] } , |
where A0 = exp[i(2p D1 / l ) ]. So the question of whether the amplitude at y1 on the image screen will be bright due to constructive interference or faint as a result of destructive interference comes down to a question of what the phase difference is between the two distances D1 and D2 where,
| Dj | º | [ ( Yj - y1 )2 + Z2 ]1/2 |
| = | [ Z2 + y12 - 2 y1 Yj + Yj2 ]1/2 | |
| = | L [ 1 - ( 2 y1 Yj )/L2 + Yj2/L2 ]1/2 , |
| L | º | [ Z2 + y12 ]1/2 . |
Utility of FFT Techniques Now, let's rewrite equation (1) to take into account many more than just two points along the aperture. That is,
| A (y1) | = | S aj exp[ i ( 2p Dj/ l + fj ) ] |
| = | S aj [ cos( 2p Dj/ l + fj ) + i sin( 2p Dj/ l + fj ) ] , |
| A (y1) | = | S aj exp[ i ( 2p Dj/ l ) ] |
| = | S aj [ cos( 2p Dj/ l ) + i sin( 2p Dj/ l ) ] , |
where, in both equations, the summation is taken over all "j" elements of light along the aperture, and to simplify typing we have replaced a(Yj) with aj . If | Yj / L | << 1, we can drop the quadratic term in favor of the linear one in expression (3) and deduce that,
| Dj | » | L [ 1 - 2 y1 Yj / L2 ]1/2 |
| » | L [ 1 - y1 Yj / L2 ] . |
Hence, equation (6) becomes,
| A (y1) | » | A0 S aj exp{ - i [ 2p y1 Yj / ( lL ) ] } |
| = | A0 S aj { cos[ 2py1 Yj / ( lL ) ] - i sin[ 2p y1 Yj / ( lL ) ] } , |
where, now, A0 = exp[i(2p L / l ) ]. When written in this form, it should immediately be apparent why discrete Fourier transform techniques (specifically FFT techniques) are useful tools for evaluation of the complex amplitude A.
(If it is not immediately apparent to you how expression [8] can be adapted to FFT techniques, click here for an explicit demonstration.)
Analytical Result
If we consider the limit where the aperture shown in Figure I.1 is divided into an infinite number of divisions, then we can convert the summation in equation (6) or (8) into an integral running between the limits, Y2 and Y1. Specifically, equation (8) becomes,
| A (y1) | » | A0 a0 | ò | exp{ - i [ 2p y1 Y / ( lL ) ] } dY , |
where, again, we have returned to the case where the aperture is assumed to be uniformly bright and set a(Y) = a0 dY. (It should be understood that a0 is the brightness of the aperture per unit length.) If we now make the substitution,
| q | º | ( 2 p y1 Y ) / ( l L ) , |
equation (9) takes the form,
| A (y1) | » | A0 [ a0 w ] ( 2 b1 )-1 | ò | exp{ - i q } dq , |
| b1 | º | p y1 ( l L )-1 [ Y1 - Y2 ] = p y1 w ( l L )-1 , |
| J1 | º | p y1 ( l L )-1 [ Y1 + Y2 ] . |
| A (y1) | » | ( - i )-1 A0 [ a0 w ] ( 2 b1 )-1 | [ exp( - i q1 ) - exp( - i q2 ) ] |
| = | i A0 [ a0 w ] ( 2 b1 )-1 exp( - i J1 ) [ exp( - i b1 ) - exp( + i b1 ) ] | ||
| = | [ A0 a0 w exp( - i J1 ) ] [ ( sin b1 ) / b1 ] . | ||
| = | A0 a0 w e( - i J1 ) sinc ( b1 ) . | ||
The last two lines of equation (13) have been derived by realizing that, for any angle c,
| e( - i c ) - e( + i c ) | = | - 2 i sin( c ) , | |
| sinc( c ) | º | sin( c ) / c . | |
Notice that if the center of the aperture is used to define the origin of the Y (and y) coordinate axis so that Y2 = - Y1, as illustrated in Figure I.1, then J1 = 0 and the amplitude A has no complex component. If the aperture is not centered as depicted in Figure I.1, then the angle J1 simply serves to introduce a phase shift in the evaluation of A.
Although this problem was solved for a specific location y1 on the image screen, we see that the sinc function solution can readily be evaluated for any other location on the screen without having to redo the integral.