- "Model A"
Initial configuration is an axisymmetric, n = 3/2 polytrope with differential rotation prescribed in such a way that the angular momentum as a function of cylindrical R has the same function as a uniformly rotating, n = 0 polytrope, that is, as a Maclaurin spheroid. (Thus, this model sits on the n' = 0 sequence, as defined by Bodenheimer & Ostriker [1973, ApJ, 180, 159].) Initial value of T/|W| = 0.30. (More information is given in Table 3.1 of Cazes' dissertation, or in Table 1 of CT00.])- MOVIE of initial instability as viewed from an inertial reference frame.
- Radial: The model was evolved on a cylindrical grid that contained 128 radial zones, but the equatorial radius of the initial axisymmetric model extended out to only zone 53. Hence, ample room was allowed for radial expansion of the model as it deformed into a barlike configuration.
- Vertical: Although the model was initially quite flat, meaning that the vertical extent above its equatorial plane was substantially less than 53 vertical zones, it was evolved on a grid that contained 128 vertical zones in this "northern" hemisphere. (Our technique for solving the Poisson equation imposed this grid size.) We assumed reflection symmetry through the equatorial plane, so it was not necessary to include an additional 128 zones in the "southern" hemisphere.
- Azimuthal: In the azimuthal direction, each grid zone had an angular extent of (2\pi) /256. However, by enforcing the evolution to maintain a two-fold "pi-symmetry", only 128 grid zones were required to evolve the system with this resolution.
This initially axisymmetric configuration is dynamically unstable toward the development of a so-called bar-mode instability; actually, the unstable eigenfunction has a slight two-armed spiral character. Here is the movie that shows the nonlinear development of this instability:

[This Quicktime movie is 5.907 MBytes in size.]This evolution is viewed from the inertial frame of reference. After "ejecting" a small portion of its mass into a "circumstellar" disk/ring, the model settles down into a nearly steady-state, rotating bar-like configuration that, for all intents and purposes is a compressible analog of a Riemann ellipsoid. (This is the theme of the CT00 paper, mentioned above.)
- MOVIE of nearly steady-state bar viewed from a rotating frame of reference.
- "Pi-symmetry" constraint removed, so the grid size was increased from 128 to 256 zones in azimuthal direction. This permitted odd azimuthal modes to develop, if they were inclined to do so.
In order to illustrate how close this configuration was to a steady-state system, Cazes shifted the simulation into a frame of reference that was rotating with the pattern speed of the bar, then extended the evolution for several more pattern rotation periods. Here is the movie showing this segment of the evolution from a frame that is rotating with the bar's overall pattern speed:

[This Quicktime movie is 7.169 MBytes in size.]For additional properties of this system, both at the start and at the end of this movie, see Table 2 of CT00.
- MOVIE of "cooling evolution" in rotating reference frame.
Cazes then "cooled" this steady-state model in a manner that is described in Chapter 5 of his dissertation. (This portion of the simulation has not been submitted for formal publication.) Here is a movie illustrating the last phase of this cooling evolution:

[This Quicktime movie is 8.514 MBytes in size.]A more detailed discussion of this "cooling" evolution is presented on the following URL: http://www.phys.lsu.edu/astro/movie_captions/fission.html. A few additional movie sequences that illustrate the internal flow of this system can also be found linked to this URL.
- MOVIE of initial instability as viewed from an inertial reference frame.
- "Model B"
Initial configuration is an axisymmetric, n = 3/2 polytrope with differential rotation prescribed in such a way that it has uniform vortensity, where vortensity is defined as the ratio of vorticity to surface density. Strictly speaking, this is how the specific angular momentum was defined as a function of cylindrical R in the equatorial plane of the configuration then, as a function of Z, the angular velocity was initially constant. Initial value of T/|W| = 0.282. (More information is given in Table 3.1 of Cazes' dissertation, or in Table 1 of CT00.])- MOVIE of initial instability in inertial reference frame.
This initially axisymmetric configuration is dynamically unstable toward the development of a so-called bar-mode instability. You'll note, however, that in this case the unstable eigenfunction has much less of a spiral character than "Model A," shown above. Here is the movie that shows the nonlinear development of this instability as viewed from the inertial reference frame:

[This Quicktime movie is 10.8 MBytes in size.]This model also settles down into a nearly steady-state, rotating bar-like configuration that, for all intents and purposes is a compressible analog of a Riemann ellipsoid. It evolves to this configuration with much less fan-fare, however; very little mass or angular momentum is shed in the equatorial plane. This indicates to us that the initially selected distibution of angular momentum in this model (uniform vortensity) is fairly well suited to a barlike configuration.
- MOVIE of nearly steady-state bar viewed from a rotating frame of reference.
In order to illustrate how close this configuration was to a steady-state system, Cazes shifted the simulation into a frame of reference that was rotating with the pattern speed of the bar, then extended the evolution for several more pattern rotation periods. Here is the movie showing this segment of the evolution:

[This Quicktime movie is 14.1 MBytes in size.]For additional properties of this system, both at the start and at the end of this movie, see Table 3 of CT00.
- Cooling evolution.
This "Model B" was never cooled.
- MOVIE of initial instability in inertial reference frame.
- "Model C_low_res"
Here, using his own self-consistent-field code, Shangli Ou created an initial model that was as close as possible to the same structure as Cazes' "Model B." That is, the initial configuration is an axisymmetric, n = 3/2 polytrope with differential rotation prescribed in such a way that it has uniform vortensity. Like Cazes' model, this model had relatively low spatial resolution. But it was run using Patrick Motl's version of our hydrocode (using mpi) on LSU's IBM SP3 computer. Initial value of T/|W| = 0.305.- MOVIE of initial instability as viewed from an inertial reference frame.
- Radial: The model was evolved on a cylindrical grid that contained 130 radial zones, but the equatorial radius of the initial axisymmetric model extended out to only zone 100. This put slightly better radial resolution than Cazes' model, but left less room in the grid for radial expansion.
- Vertical: Because we are now using Howard Cohl's version of the Poisson solver, we no longer have to place the vertical boundary as far from the coordinate origin as the radial boundary. Here, we use 130 vertical zones and include both the southern and northern hemispheres in the computational grid. A approximately 75 grid zones fell within the model, leaving considerable room for vertical expansion, if necessary.
- Azimuthal: In the azimuthal direction there are 128 zones spread over the entire 2\pi range of angles, that is, "pi-symmetry" is not enforced during this evolution. Hence this model has half the azimuthal resolution as Cazes' Model B.
This initially axisymmetric configuration is dynamically unstable toward the development of a so-called bar-mode instability. Here is the movie that shows the nonlinear development of this instability, as viewed from the inertial reference frame:

[This Quicktime movie is 17.4 MBytes in size.]This model's evolution is similar to Cazes' Model B evolution. Its differences can be attributed to two things: (a) This model has a higher initial value of T/|W|, so it has more of a spiral eigenfunction and its nonlinear deformation is a bit more severe. (b) This model filled a larger fraction of the grid (radially) initially, so when it expanded, it hit the edge of the grid and some of the mass/angular momentum was lost off of the grid.
- MOVIE of "cooling evolution" in rotating reference frame.
Shangli "cooled" this model in the same manner as John Cazes had cooled his "model A" earlier. But he cooled it a bit more slowly than the earlier model. Here is a movie illustrating this entire "cooling" evolution as viewed from a frame rotating with the initial pattern frequency of the bar:
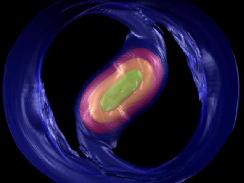
[This Quicktime movie is 12.946 MBytes in size.]Note, as of 28 July 2002, we have not finished evolving this system. It looks like the "binary" amplitude is still slowly growing and, as expected, the pattern frequency is continuing to get higher as the system contracts.
- MOVIE of initial instability as viewed from an inertial reference frame.
- "Model D_high_res"
Here, using his own self-consistent-field code, Shangli Ou created an initial model that was as close as possible to the same structure as Cazes' "Model B." That is, the initial configuration is an axisymmetric, n = 3/2 polytrope with differential rotation prescribed in such a way that it has uniform vortensity. Like Cazes' model, this model had relatively low spatial resolution. But it was run using Patrick Motl's version of our hydrocode (using mpi) on the IBM SP3 computer at the San Diego Supercomputing Center. Initial value of T/|W| = 0.277.- Initial instability in inertial reference frame.
- Radial: The model was evolved on a cylindrical grid that contained 258 radial zones, but the equatorial radius of the initial axisymmetric model extended out to only zone 140. Hence, ample room was allowed for radial expansion of the model as it deformed into a barlike configuration.
- Vertical: Because we are now using Howard Cohl's version of the Poisson solver, we no longer have to place the vertical boundary as far from the coordinate origin as the radial boundary. Here, we use 162 vertical zones and include both the southern and northern hemispheres in the computational grid. Approximately 120 grid zones fell within the model, leaving considerable room for vertical expansion, if necessary.
- Azimuthal: In the azimuthal direction there are 256 zones spread over the entire 2\pi range of angles, that is, "pi-symmetry" is not enforced during this evolution.
This initially axisymmetric configuration is dynamically unstable toward the development of a so-called bar-mode instability. Here is the movie that shows the nonlinear development of this instability, as viewed from the inertial reference frame:

[This Quicktime movie is 10.264 MBytes in size.]Note that as of 28 July 2002, we are still running this evolution. It looks like the system is near its steady-state configuration and is therefore is almost ready to "cool."
- Initial instability in inertial reference frame.