Computer-Generated Holography (CGH)
September 05, 1999
PHYS4412 (Computational Science II)
Department of Physics & Astronomy
Louisiana State University
PHYS4412 (Computational Science II)
Department of Physics & Astronomy
Louisiana State University
| III.C | Triangular Aperture |
|---|
Setup
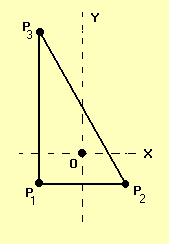
Consider any three points in space -- P1, P2, and P3 -- that do not lie on a straight line. From elementary Euclidian geometry we know that these three points define a plane. They also can be used to specify the vertices of a flat triangular aperture that lies in this plane.
| Figure III.1 |
|---|
 |
We will refer to the Cartesian coordinate system defined in this way as the aperture coordinate system. In the aperture coordinate system, the (x,y,z) coordinate location of each vertex is:
| P1 | = | ( x1, y1, 0 ) , | ||
| P2 | = | ( x1, y1, 0 ) , | ||
| P3 | = | ( x3, y3, 0 ) | = | ( x1, y3, 0 ) . |
In the aperture coordinate system, the equation for the line that connects vertices P3 and P2, and thereby forms the "upper" edge of the triangular aperture is,
| yupper | = | y3 - [ ( y3 - y2 ) / ( x3 - x2 ) ] ( x3 - x ) |
| = | y3 - [ ( y3 - y2 ) / ( x1 - x2 ) ] ( x1 - x ) , |
and the equation for the line that connects vertices P1 and P2, and thereby forms the "lower" edge of the triangular aperture is,
| ylower | = | y1 - [ ( y1 - y2 ) / ( x1 - x2 ) ] ( x1 - x ) . |
Analytical Result
By analogy with earlier chapters, if the triangular aperture is assumed to be uniformly bright (i.e., aj,k = a0 dx dy, and a0 is the brightness per unit area), and the phase f = 0 at all locations on the aperture, then at any position in space (xa,ya,za) as measure in the aperture coordinate system from the aperture origin (as illustrated above in Fig. III.3),
| A (xa,ya,za) | » | A0 a0 | ò | exp{ - i [2p xax / (lL)]} dx | ò | exp{ - i [2p yay / (lL)]} dy , |
| L | º | [ xa2 + ya2 + za2 ]1/2 . |
Both of these integrals can be completed in the same fashion as described in earlier chapters for the 1D slit or for the 2D rectangular aperture, but now some care must be taken in establishing the limits of integration because along two of the edges of the triangular aperture, the limiting values of "y" are now a function of the x-coordinate. Specifically, the integral over y must be performed between the limits ylower and yupper, as defined above by Equations (2) and (3), while the integral over x is carried from xlower = x1 and xupper = x2.
Completing the integrals with these limits gives,
| A (xa,ya,za) | » | i [ A0 a0 [ ( x2 - x1 ) ( y3 - y1 ) / 2 ] ] exp( - i nx0 ) exp( - i my0 ) |
| { [ exp( - i b ) / ( 2 b ) ] sinc aupper - [ exp( + i b ) / ( 2 b ) ] sinc alower } , | ||
where,
| aupper | º | (1/2)n ( x2 - x1 ) + (1/2)m ( y2 - y3 ) , |
| alower | º | (1/2)n ( x2 - x1 ) + (1/2)m ( y2 - y1 ) , |
| b | º | (1/4)m ( y3 - y1 ) , |
| x0 | º | (1/2) ( x1 + x2 ) , |
| y0 | º | (1/2) [ y2 + (1/2) ( y1 + y3 ) ] , |
| n | º | [ 2p / ( lL ) ] xa , |
| m | º | [ 2p / ( lL ) ] ya . |
Discussion
When comparing equation (6) to equation (I.B-7) -- which is the result for a rectangular aperture -- we see several significant differences: First, because aupper is not equal to alower, we are unable to combine the terms containing b into a sinc function. (See, however, what happens when ya = 0, as discussed below.) Second, in order for the leading phase factor to disappear, we must define the vertical position of the origin of the aperture coordinate system (point "O" in Figure III.1) such that y2 = - (1/2) ( y1 + y3 ). Finally, the area multiplying the surface brightness, a0, is appropriately the area of the triangle.
The analytical expression (6) formally poses a problem when ya = 0 ( m = b = 0 ) because of division by zero. However, when m = 0, aupper = alower so the terms involving b can be combined into a sinc function as follows,
| A (xa,ya,za) | » | A0 a0 [ ( x2 - x1 ) ( y3 - y1 ) / 2 ] exp( - i nx0 ) [ sinc(a) sinc(b) ] |
| = | A0 a0 [ ( x2 - x1 ) ( y3 - y1 ) / 2 ] exp( - i nx0 ) [ sinc(a) ] , |
where the last line results from the fact that sinc(0) = 1.
Two right triangles make a rectangle
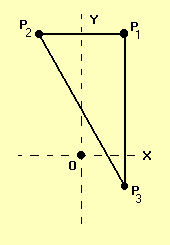
In an effort to partially check the validity of Eq. (6), let's set y2 = y1 so that the triangle becomes a right triangle (as shown here in Figure III.2a), then "add" it to the complementary triangle (see Figure III.2b) that shares its hypotenuse and can be used to make a complete rectangle with sides w = ( x2 - x1 ) and h = ( y3 - y1 ). More specifically, in the aperture coordinate system, the three vertices of second aperture should have the following coordinates:
| P1 | = | ( x1 + w, y1 + h, 0 ) , |
| P2 | = | ( x1, y1 + h, 0 ) , |
| P3 | = | ( x1 + w, y1, 0 ) . |
For the aperture shown in Fig. III.2a, then,
| aupper | º | (1/2)n w + (1/2)m ( - h ) , |
| alower | º | (1/2)n ( w ) , |
| b | º | (1/4)m ( h ) , |
| x0 | º | x1 + (1/2) w , |
| y0 | º | y1 + (1/4) h , |
| n | º | [ 2p / ( lL ) ] xa , |
| m | º | [ 2p / ( lL ) ] ya , |
so,
| A III.2a | » | i A0 a0 [ wh/2 ] exp( - i nx1 ) exp( - i n w/2 ) exp( - i my1 ) exp( - i m h/4 ) |
| [ 2 / mh ] { [ exp( - i m h/4 ) ] sinc [ (1/2)n w - (1/2)m h ] - [ exp( + i m h/4 ) ] sinc [ (1/2)n w ] } | ||
| = | i A0 a0 [ wh/2 ] exp( - i nx1 ) exp( - i n w/2 ) exp( - i my1 ) exp( - i m h/4 ) [ 2 / mh ] | |
| { [ exp( - i m h/2 ) ] sinc [ (1/2)n w - (1/2)m h ] - sinc [ (1/2)n w ] } . | ||
| Figure III.2 | |
|---|---|
 |
 |
| a | b |
And for the aperture shown in Fig. III.2b,
| aupper | º | (1/2)n ( - w ) + (1/2)m h , |
| alower | º | (1/2)n ( - w ) , |
| b | º | (1/4)m ( - h ) , |
| x0 | º | x1 + (1/2) w , |
| y0 | º | y1 + (3/4) h , |
| n | º | [ 2p / ( lL ) ] xa , |
| m | º | [ 2p / ( lL ) ] ya , |
so,
| A III.2b | » | i A0 a0 [ wh/2 ] exp( - i nx1 ) exp( - i n w/2 ) exp( - i my1 ) exp[ - i m ( 3h/4 ) ] |
| [ 2 / mh ] { - [ exp( + i m h/4 ) ] sinc [ (1/2)n w - (1/2)m h ] + [ exp( - i m h/4 ) ] sinc [ (1/2)n w ] } | ||
| = | i A0 a0 [ wh/2 ] exp( - i nx1 ) exp( - i n w/2 ) exp( - i my1 ) [ 2 / mh ] | |
| { - [ exp( - i m h/2 ) ] sinc [ (1/2)n w - (1/2)m h ] + [ exp( - i m h ) ] sinc [ (1/2)n w ] } . | ||
Adding the two together, we obtain,
| A III.2a + III.2b | » | i A0 a0 [ wh/2 ] exp( - i nx1 ) exp( - i n w/2 ) exp( - i my1 ) [ 2 / mh ] |
| sinc [ (1/2)n w ] { exp( - i m h ) - 1 } | ||
| = | i A0 a0 [ wh ] exp( - i nx1 ) exp( - i n w/2 ) exp( - i my1 ) exp( - i m h/2 ) [ 1 / mh ] | |
| sinc [ (1/2)n w ] { exp( - im h/2 ) - exp( + i m h/2 ) } | ||
| = | i A0 a0 [ wh ] exp[ - i n ( x1 + w/2 ) ] exp[ - i m ( y1 + h/2 ) ] | |
| sinc [ (1/2)n w ] sinc [ (1/2)m h ] . | ||
This is, indeed, the correct expression for the complex amplitude of a rectangular aperture of width "w" and height "h".